Mathematics and Science are inextricably linked. As the renowned twentieth-century physicist Eugene Wigner wrote, mathematics is "unreasonably successful" in the natural sciences. By this he meant that it seems our entire world is seemingly beholden to the workings of mathematical laws.
Our most fundamental theories are complex systems of dense mathematical formulations that predict the behavior of the world around us so precisely that we’re able to peer into the earliest moments, right after the Big Bang itself and understand the workings of even the most extreme bending of space and time around black holes. Students of physics and the related sciences study these formulations and the mathematics they rely on for years, relentlessly working to gain mastery—and if they’re lucky—some intuition for the behaviors of complex, dynamical systems.
Yet, perhaps this relationship between math and science goes even deeper. Perhaps modern science and the scientific method itself do more than rely on mathematics. Perhaps—in no metaphorical sense—they are mathematics made manifest.
The Magic of Curves on the Plane
When Isaac Newton discovered Calculus alongside Gottfried Leibniz in the late seventeenth century, they arguably ushered in the modern world. However on a technical level, what the study of calculus enabled was the ability for mathematics, as a discipline, to rigorously study change. Without wishing to dig up uncomfortable memories of math class, I will attempt to summarize in one sentence the purpose of the entire field of differential calculus. Simply put, rather than like the operations of arithmetic that describe what happens to a quantity when one combines or dissects it, a new kind of operation—the derivative—enables mathematicians to study how, and how quickly, a quantity changes over time (like the velocity of a ball rolling down a slope) or over space (like how weather patterns vary by region).
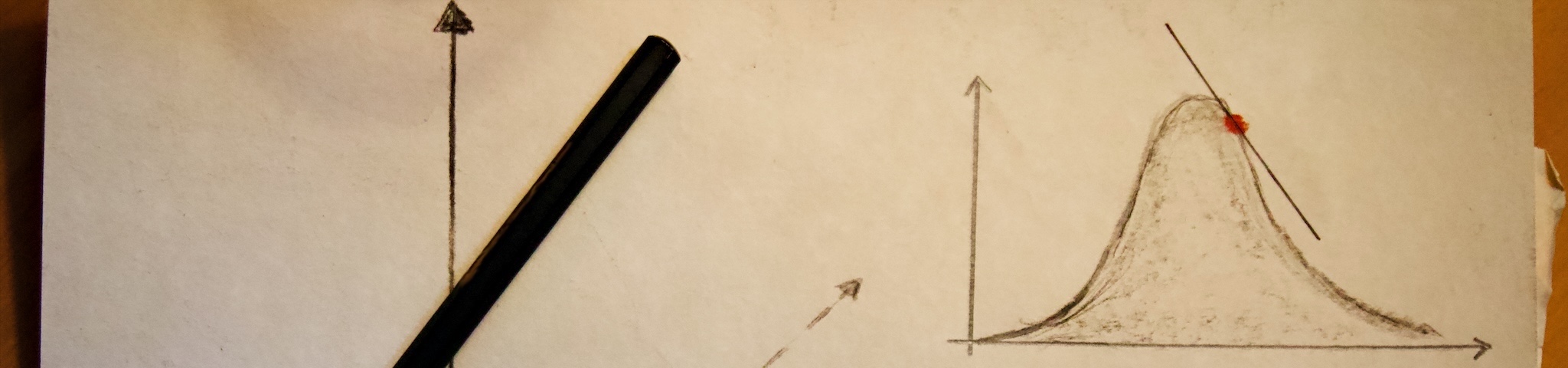
Now, even that one sentence was a lot to take in, so if you take nothing else from this section, let it be this: a derivative measures the rate of change. Often times however, a system is complex and can change in multiple ways at once. Consider a system far more complex than a ball on a hill: the human body. No matter how much we as a society might wish it to be true, healthy living is not a simple function of one variable. There are lots of factors that can affect a person’s health and each does so in a different way. Exercise is good for you, but so is maintaining a good diet and not smoking. A myriad of factors, both known and unknown, affect overall health—including sheer dumb luck. But how are we to make sense of this tangled knot of cause and effect?
Enter, the modern scientific method and the randomized controlled clinical trial.
Empirical Meets Theoretical
Researchers looking to tease apart the effects of a new diet plan on patient’s overall health could choose to assemble a group of people who all share the same socioeconomic background, are around the same age, the same height and weight, and who exercise around the same amount of time every week. Since these factors are held in common, they can be assumed to affect all of the participants equally and thus factors like height, weight, wealth, and exercise are held constant or controlled for during the time of the experiment. The researchers will then divide the group in two, giving one half the novel diet plan and the other a more traditional and well researched plan to act as a control. Thus, the only factor which is free to vary between the groups, their diet, is finally made available to study.
In effect, this method allows the researchers to—in principle—assume all other factors remain constant and our complex system of multiple variables has been simplified into a simple function of one. Measuring the ensuing rate of change is then an empirical derivative, allowing us to ascertain the nature of the change we’ve just caused.
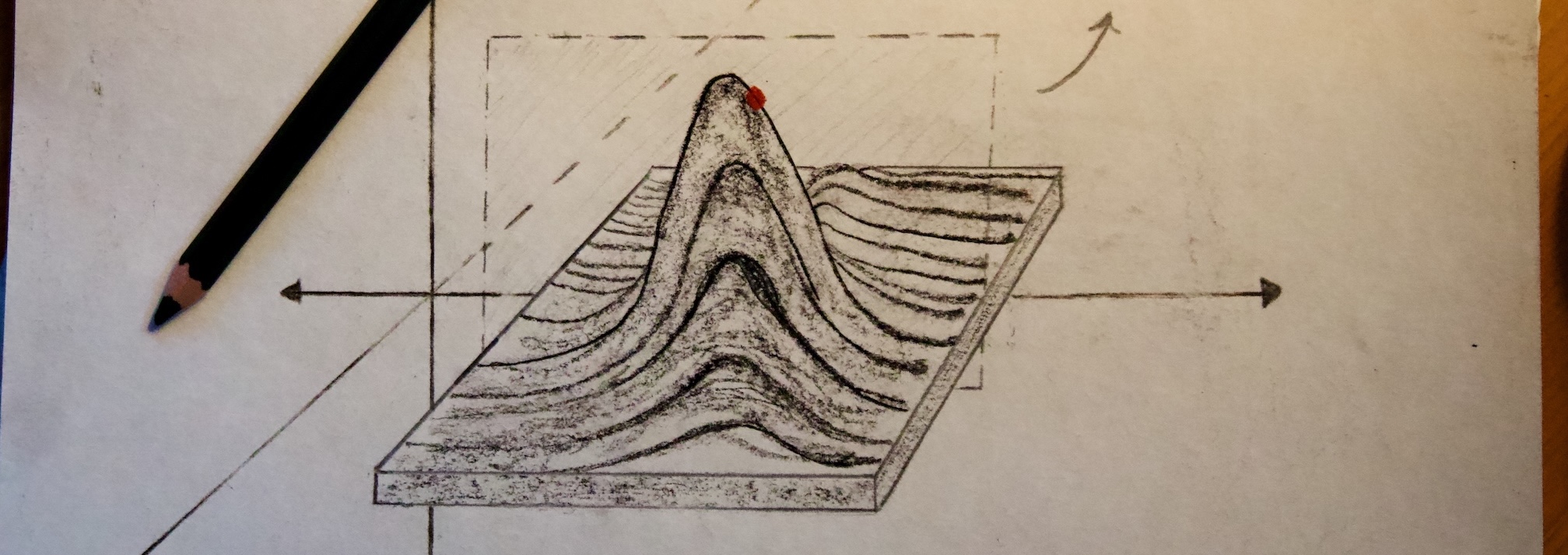
This example is more than analogous to mathematics. Advanced students of mathematics study increasingly complex systems and to do so must learn to take something called a partial derivative—which sadly is not any simpler, despite how it may sound. These systems combine several interdependent variables and thus our math students employ the same process as our researchers above.
To take a partial derivative, one must arrange the given system of equations in such a way as to tease apart the influence of each variable and then assume that each can be held constant at the point under consideration with respect to the variable in question. Using different tools the mathematician performs the exact same process as our heath researchers. Where mathematicians deal with systems of abstract equations, our public health scientists do the same with the messy particulars of real life.
None of this is to suggest that economists, public health researchers, and other participants in the empirical sciences do not also use the mathematical techniques of calculus and derivatives in conjunction with their work—of course they do, and in spades. Instead, the point here is to examine how the theoretical methods of advanced math and the practical techniques of scientists today are both really one and the same. The technique of performing a randomized clinical trial works precisely because it is fundamentally an implementation of mathematical theory, a real-world implementation of the work of mathematics. Randomized controlled clinical trial are the act of taking a partial derivative in tangible form and in that way they are the physical incantation of those same discoveries made by Newton and Leibniz all those centuries ago.
